Dipping into Processing.js to create the abstract background for this site was one of the most exciting parts of this design. Almost the perfect combination of art, programming and play. Processing allows you to get interesting results with a minimum amount of code.

I went through a few different iterations to get to the final abstract you see above, one of the key elements are the cross/plus signs which contrast with the circles.

Random circles are fairly simple, but when it comes to drawing something with edges, you have to work in an amount of random rotation in order to generate chaos from order.

As it turns out, rotation in Processing.js works in a pretty unexpected way, and it took a while for me to get shapes accurately rotating around their x and y coordinates.

An Example…

Let's start with the following code:

void setup()
{
  size(660, 228);
  noLoop();

  noStroke();
  rectMode(CENTER);
  drawSquares();
}

void drawSquares()
{
  int x = y = 24;
  for (int i=1; i <= 108; i++) {

    fill(200,200,200);
    rect(x, y, 24, 24);

    fill(100,100,100);
    ellipse(x, y, 4, 4);

    if (x == 636) {
      x = 24;
      y = y+36;
    } else {
      x = x+36;
    }
  }
}

In the setup function, we set the canvas size, stop the loop (so there is no animation), turn off strokes, set the rectangle mode to center and call the drawSquares function.

Within drawSquares() we set a starting x and y coordinate, then loop round 108 times. Each time we set the fill colour of the rectangle, draw the rectangle, and then mark the center with a small, different colour circle. Finally we work out where to go next, if we are on the last horizontal rectangle (x == 636) then we drop to the next row by adding 36 to y.

We end up with something that looks like:

The next step is to rotate each rectangle around their own center point (marked by the little circle). Let's use the rotate function to get the job done:

for (int i=1; i <= 108; i++) {

  rotate(0.4+TWO_PI/360);

  fill(200,200,200);
  rect(x, y, 24, 24);

  // Snip...
}

Well, that looks pretty cool, but it's not exactly what we would of been hoping for.

The key to understanding why this happens is in the documentation of rotate()

Technically, rotate() multiplies the current transformation matrix by a rotation matrix. This function can be further controlled by the pushMatrix() and popMatrix().

Well, that hasn't made things much clearer. Delving deeper into either the pushMatrix or popMatrix documentation finally starts to shed some light on the matter.

Calling rotate() actually rotates the whole coordinate system by the angle you specify, so any further drawings are then positioned on this new, transformed set of coordinates. The documentation puts it slightly more technically:

rotate() multiplies the current transformation matrix by a rotation matrix

Simple. I think. You can use pushMartix() to save the state of the current coordinate system, do the rotate and then use popMatrix() to restore the matrix back to the original.

The flow goes a little like:

// Matrix: Standard Matrix
pushMatrix() // Save the standard matrix at the top of the stack
// Matrix: Standard Matrix
rotate() // Manipulate the standard matrix
// Matrix: Rotated Matrix
popMatrix() // restore the standard matrix by popping it off the top
// Matrix: Standard Matrix

Providing we draw before the popMatrix the drawing will be on the rotated coordinates, but everything else after the pop will remain unchanged.

for (int i=1; i <= 108; i++) {

  pushMatrix();

  rotate(0.4+TWO_PI/360);

  fill(200,200,200);
  rect(x, y, 24, 24);

  popMatrix();

  // Snip...
}

And with that, problem solved!

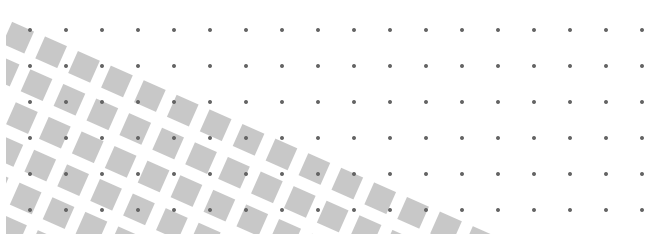
Okay, so not quite problem solved, it's closer, all of the squares are rotated consistently and the circles are in the correct grid, but they aren't lined up at all. One last tweak to get everything working.

Before the rotate we need to translate the matrix by the x and y coordinates that we want to rotate around (in this case it's the center of the square, marked with the little circle). After calling rotate we need to translate the matrix back to where it started using equivalent negative values.

Another illustration is in order:

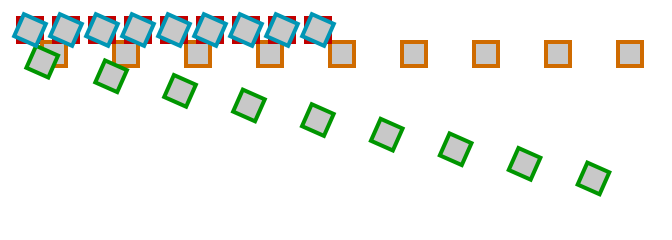
1. Red The initial draw location
2. Orange Transform the matrix using translate(x, y)
3. Green Rotate the matrix
4. Blue Transform the matrix again, this time using translate(-x, -y)

Got that? Once we put it all together we end up with:

void setup()
{
  size(660, 228);
  noLoop();

  rectMode(CENTER);
  drawSquares();
}

void drawSquares()
{
  int x = 24;
  int y = 24;

  noStroke();

  for (int i=1; i <= 108; i++) {

    pushMatrix();

    translate(x, y);
    rotate(0.4+TWO_PI/360);
    translate(-x, -y);

    fill(200,200,200);
    rect(x, y, 24, 24);

    popMatrix();

    fill(100,100,100);
    ellipse(x, y, 4, 4);

    if (x == 636) {
      x = 24;
      y = y+36;
    } else {
      x = x+36;
    }
  }
}

Which brings us to our final example. Perfect!

All five of these examples, including the complete code are available at the accompanying example page.

Done.